人工智能课程设计报告-N皇后问题
人工智能课程设计报告
- 班级:____________________
- 姓名:____________________
- 学号:____________________
- 指导教师:赵曼
- 2015年11月
课程背景
人工智能(Artificial Intelligence),英文缩写为AI。它是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。 人工智能是计算机科学的一个分支,它企图了解智能的实质,并生产出一种新的能以人类智能相似的方式做出反应的智能机器,该领域的研究包括机器人、语言识别、图像识别、自然语言处理和专家系统等。人工智能从诞生以来,理论和技术日益成熟,应用领域也不断扩大,可以设想,未来人工智能带来的科技产品,将会是人类智慧的“容器”。
人工智能是对人的意识、思维的信息过程的模拟。人工智能不是人的智能,但能像人那样思考、也可能超过人的智能。
人工智能是一门极富挑战性的科学,从事这项工作的人必须懂得计算机知识,心理学和哲学。人工智能是包括十分广泛的科学,它由不同的领域组成,如机器学习,计算机视觉等等,总的说来,人工智能研究的一个主要目标是使机器能够胜任一些通常需要人类智能才能完成的复杂工作。但不同的时代、不同的人对这种“复杂工作”的理解是不同的。
人工智能是计算机学科的一个分支,二十世纪七十年代以来被称为世界三大尖端技术之一(空间技术、能源技术、人工智能)。也被认为是二十一世纪三大尖端技术(基因工程、纳米科学、人工智能)之一。这是因为近三十年来它获得了迅速的发展,在很多学科领域都获得了广泛应用,并取得了丰硕的成果,人工智能已逐步成为一个独立的分支,无论在理论和实践上都已自成一个系统。
人工智能是研究使计算机来模拟人的某些思维过程和智能行为(如学习、推理、思考、规划等)的学科,主要包括计算机实现智能的原理、制造类似于人脑智能的计算机,使计算机能实现更高层次的应用。人工智能将涉及到计算机科学、心理学、哲学和语言学等学科。可以说几乎是自然科学和社会科学的所有学科,其范围已远远超出了计算机科学的范畴,人工智能与思维科学的关系是实践和理论的关系,人工智能是处于思维科学的技术应用层次,是它的一个应用分支。从思维观点看,人工智能不仅限于逻辑思维,要考虑形象思维、灵感思维才能促进人工智能的突破性的发展,数学常被认为是多种学科的基础科学,数学也进入语言、思维领域,人工智能学科也必须借用数学工具,数学不仅在标准逻辑、模糊数学等范围发挥作用,数学进入人工智能学科,它们将互相促进而更快地发展。
题目二:N 皇后问题
问题描述
分别用回溯法(递归)、遗传算法(GA)和CSP 的最小冲突法求解 N 皇后问题。
问题定义:如何在 n * n 的国际象棋棋盘上放置 n 个皇后,使得任意一个皇后都无法直接吃掉其他皇后?
即:任意两个皇后不能处于同一行、同一列或同一条对角线上。
要求:
ⅰ. 输入 n,比较几种算法在相同规模问题下的运行时间,并列表给出结果。
ⅱ. 比较同一算法在 n 不同时的运行时间,分析其时间复杂性,并列表给出结果。
示例:八皇后问题的一个有效解。
二、算法分析
(1)回溯法(递归)
回溯法解题的一般步骤:
- 针对所给问题,定义问题的解空间;
- 确定易于搜索的解空间结构;
- 以深度优先方式搜索解空间,并在搜索过程中使用剪枝函数避免无效搜索。
实现细节:
- 使用一维整型数组
col[]存放结果:col[i]表示第i列的皇后位于第col[i]行。 - 引入三个辅助数组表示当前状态:
a[i] = 0:表示第i行无皇后;b[i] = 0:表示反斜线/(行号 + 列号 = 常数)上无皇后;c[i] = 0:表示正斜线\(行号 - 列号 + n - 1 = 常数)上无皇后。
初始时所有数组为 0。放置皇后时标记对应行与对角线;回溯时清除标记。当回溯至第 0 列时,说明已找到全部解,程序结束。
(2)遗传算法(GA)
遗传算法的基本运算过程如下:
a) 初始化:设进化代数计数器 t = 0,最大进化代数 T,随机生成 M 个个体作为初始种群 P(0)。
b) 个体评价:计算种群 P(t) 中每个个体的适应度(如:适应度 = 1 / (1 + \text{冲突数}))。
c) 选择运算:基于适应度选择优秀个体,用于遗传或交叉。
d) 交叉运算:对选中个体应用交叉算子(如 PMX),生成新后代。
e) 变异运算:以小概率对个体的某些基因位进行随机变异。
f) 终止判断:若 t = T,则输出进化过程中适应度最高的个体作为最优解,终止计算。
(3)CSP 最小冲突法(Min-Conflicts)
算法步骤:
- 初始化:随机放置 n 个皇后(允许冲突);
- 迭代优化:
- 任选一个存在冲突的皇后;
- 尝试将其移动到当前行(或列)的其他位置;
- 选择使冲突数最少的新位置;
- 终止条件:冲突数为 0,或达到最大迭代次数。
2. 数据结构
- 一维数组:用于存储皇后位置(如
col[n])、行/对角线占用状态(a[],b[],c[])等。
- 二维数组:可选,用于可视化棋盘状态(如
board[n][n]),但非必需。
三、算法设计
1.回溯搜索
//回溯搜索
void Function1::DFS(int t,bool isShowTime)
{
if (t == n)//说明已经排了n行了(从0开始的),即排列结束了
{
for (int i = 0; i<n; i++)
{
rec[i] = board[i];
}
if (! isShowTime )PrintChessBoard();//输出棋局
count++;
return;
}
for (int i = 0; i<n; i++)
{
//有冲突
if (ver[i] == 1||ru[i - t + n] == 1||rd[i + t] == 1) continue;
//没有冲突
ver[i] = 1;
ru[i - t + n] = 1;
rd[i + t] = 1;
board[t] = i;
DFS(t + 1, isShowTime);//深搜递归
//后退处理
rd[i + t] = 0;
ru[i - t + n] = 0;
ver[i] = 0;
}
return;
}
2.遗传算法
void CGAQueen::PrintChessBoard(bool PrintChessBoard)
{
bool DisplayAllAnsures=PrintChessBoard;//是否输出所有棋盘结果
int g = 0, num = 0;
InitialPopulation();
while (g == 0 && num < this->Iteration)
{
num++;
g = 0;
for (int k = 0; k < this->Population ; k++)
{
this->FillArea(k);
this->CostMatrix[k] = this->CostFunc(k);
}
this->PopulationSort();
if (this->CostMatrix[0] == 0)//已经完成计算
g = 1;
if (DisplayAllAnsures)
{
PrintTheBestAnsure();
/*for (i = 0; i <= ChessBoradLenght - 1; i++)
{
cout << "row:" << i << " col:" << this->ChromosomeMatrix[i][0] << endl;
}
cout << endl;*/
}
this->GenerateCrossOverMatrix();
this->Mating();
this->ApplyMutation();
}
cout << "实际迭代:" << num <<" 次"<< endl;
if (DisplayAllAnsures)
{
cout << "最佳答案为:" << endl;
this->PrintTheBestAnsure();
}
}
3.CSP 最小冲突算法
//用最小冲突算法调整第row行的皇后的位置(初始化时每行都有一个皇后,调整后仍然在第row行)
//调整过后check一下看看是否已经没有冲突,如果没有冲突(达到终止状态),返回true
bool CSP_Queens::Adjust_row(int row)
{
int cur_col = R[row];
int optimal_col = cur_col;//最佳列号,设置为当前列,然后更新
//计算总冲突数
int min_conflict = col[optimal_col] + pdiag[GetP(row, optimal_col)] - 1
+ cdiag[GetC(row, optimal_col)] - 1;//对角线冲突数为当前对角线皇后数减一,三次重叠了
//逐个检查第row行的每个位置,看看是否存在冲突数更小的位置
for (int i = 0; i < N; i++)
{
if (i == cur_col) continue;
int conflict = col[i] + pdiag[GetP(row, i)] + cdiag[GetC(row, i)];
if (conflict < min_conflict)
{
min_conflict = conflict;
optimal_col = i;
}
}
//如果最佳列位置改变,则皇后移向新的最小冲突位置,要更新col,pdiag,cdiag,
if (optimal_col != cur_col)
{
col[cur_col]--;
pdiag[GetP(row, cur_col)]--;
cdiag[GetC(row, cur_col)]--;
col[optimal_col]++;
pdiag[GetP(row, optimal_col)]++;
cdiag[GetC(row, optimal_col)]++;
R[row] = optimal_col;
if (col[cur_col] == 1 && col[optimal_col] == 1
&& pdiag[GetP(row, optimal_col)] == 1 && cdiag[GetC(row, optimal_col)] == 1) {
return Qualify();//qualify相对更耗时,所以只在满足上面基本条件后才检查
}
}
//否则当前点就是最佳点,一切都保持不变
return false;//如果都没变的话,肯定不满足终止条件,否则上一次就应该返回true并终止了
}
//检查冲突
bool CSP_Queens::Qualify()
{
for (int i = 0; i < N; i++){
if (col[R[i]] != 1 ||
pdiag[GetP(i, R[i])] != 1 ||
cdiag[GetC(i, R[i])] != 1) {
return false;
}
}
return true;
}
//最终用户调用函数,numOfQueens为输入皇后数,PrintChessBoard判断是否输出棋盘表示
int CSP_Queens::CSPAlgorithms(bool PrintChessBord)
{
srand((unsigned)time(NULL));
Init();
if (Qualify()) {//运气很好,初始化后就满足终止条件
if (PrintChessBord)Print_result();
return 0;
}
bool end = false;
while (!end) {
for (int i = 0; i < N; i++) {
if (Adjust_row(i)) {
end = true;
break;
}
}
}
if (PrintChessBord)Print_result();
return 0;
}
四、运行结果及分析
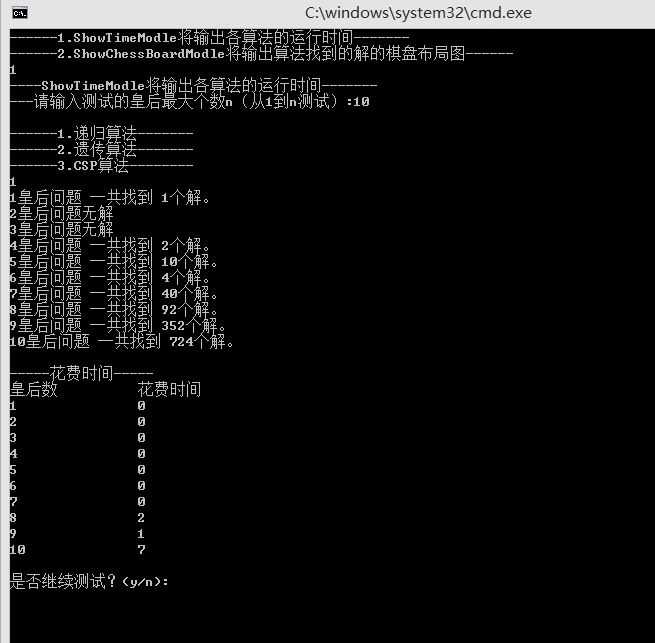
- 递归算法(回溯法)
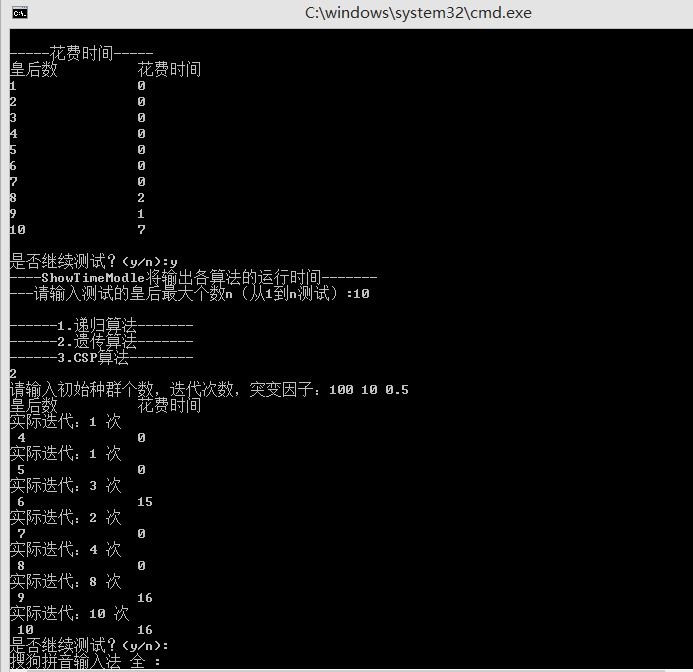
- 遗传算法
- CSP 最小冲突算法
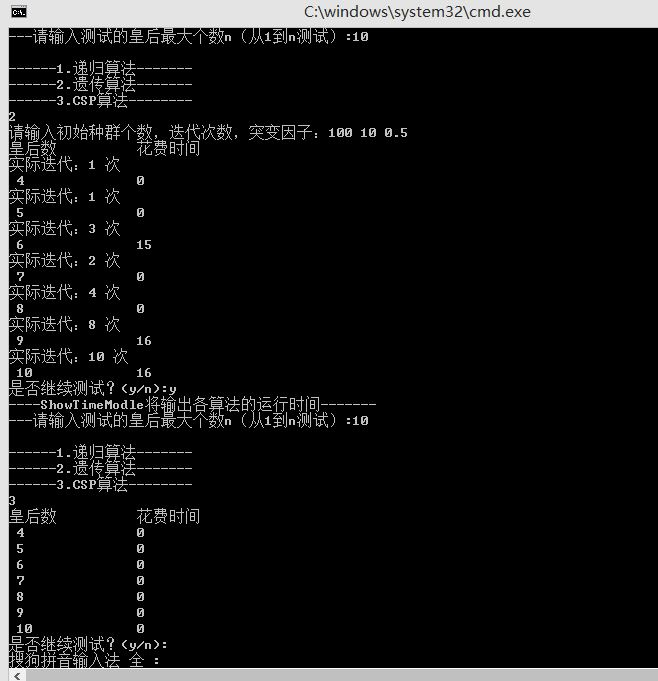
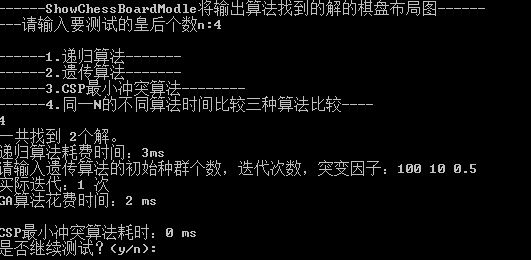
- n = 4 时不同算法的比较
- n = 8 时不同算法的比较
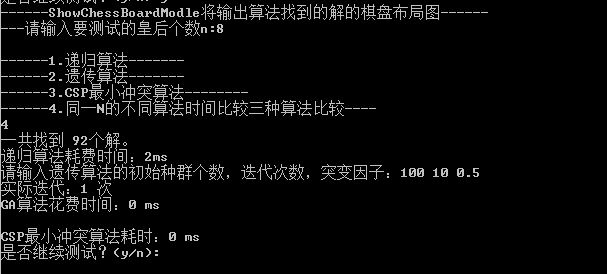
结果分析
- 回溯法:在 n 较小时效率极高,但随 n 增大呈指数级增长。当 n = 35 时已难以实用。
- 遗传算法:
- 优点:全局搜索能力强,能跳出局部最优,适用于中等规模问题;
- 缺点:收敛慢,局部搜索能力弱,运行时间受 n 影响较大;
- 在 n 较小时不如回溯法快,但在 n 增大后优势显现,可解决回溯法无法处理的问题。
- CSP 最小冲突法:
- 优点:运行速度快,时间与 n 无强相关性,尤其在 n > 100 时效率最高;
- 缺点:易陷入局部极小(如“高原”“山脊”),约 86% 的情况可能卡住,不一定总能找到解。
综合结论:
- n 很小时(如 n < 20):回溯法最优;
- n 中等(如 20 < n < 100):遗传算法适用;
- n 很大(如 n > 100):CSP 最小冲突法最高效。
总结
通过本次课程实习,我不仅加深了对回溯法、遗传算法、CSP 最小冲突法等经典搜索算法的理解,还复习了队列、栈、图、文件读写等基础知识,提升了对基本数据结构的运用能力。
在解决问题的过程中,我巩固了数据结构知识,提高了编程与调试能力,增强了编程信心。同时,也暴露出自身在算法优化和边界处理方面的不足,为今后学习提供了明确方向。
最后,衷心感谢赵曼老师的悉心指导——耐心解答疑问、指出程序缺陷,并提出切实可行的改进建议,使我的程序功能更加完善。
CSP 算法源代码:
CSPAlgorithms.h
//CSPAlgorithms.h
#pragma once
class CSP_Queens
{
public:
//构造函数,numOfQueens为输入皇后数,
CSP_Queens(int numOfQueens);
~CSP_Queens();
private:
//row[i]表示当前摆放方式下第i行的皇后数,
int *row;
//col[i]表示当前摆放方式下第i列的皇后冲突数
int *col;
int N; //放置N个皇后在N*N棋盘上
//从左上到右下的对角线上row-col值是相同的,但是这个值有可能是负值,最小为-(N-1),
//所以可以做个偏移,统一加上N-1,这样这个值就在[0,2*N-2]范围内,将这个值作为该对角线的编号
//pdiag[i]表示当前摆放方式下编号为i的对角线上的皇后数
int *pdiag;//principal diagonal,主对角线,左上到右下(表示和主对角线平行的2N-1条对角线)
//从右上到左下的对角线row+col的值相同,取值范围为[0, 2 * N - 2],2*N-1条,作为对角线编号
//cdiag[i]表示编号为i的对角线上的皇后数
int *cdiag;//counter diagonal,副对角线
//R[]用来存储皇后放置位置,R[row] = col表示(row,col)处,即“第row行第col列”有个皇后
int *R;
public:
int swap(int &a, int &b);
//给定二维矩阵的一个点坐标,返回其对应的左上到右下的对角线编号
int GetP(int row, int col);
//给定二维矩阵的一个点坐标,返回其对应的右上到左下的对角线编号
int GetC(int row, int col);
//返回begin, begin + 1, ... , end - 1 这end - begin个数中的随机的一个
int My_rand(int begin, int end);//左闭右开[begin, end)
//原地shuffle算法,算法导论中的randomize in place算法
void Randomize(int a[], int begin, int end);// 左闭右开
//初始化皇后的摆放,同时初始化row,col,pdiag,cdiag数组
void Init();
//用最小冲突算法调整第row行的皇后的位置(初始化时每行都有一个皇后,调整后仍然在第row行)
//调整过后check一下看看是否已经没有冲突,如果没有冲突(达到终止状态),返回true
bool Adjust_row(int row);
bool Qualify();
void Print_result();
//最终用户调用函数 PrintChessBoard判断是否输出棋盘表示
int CSPAlgorithms(bool PrintChessBord);
};
CSPAlgorithms.cpp
//CSPAlgorithms.cpp
#include"CSPAlgorithms.h"
#include <cstdio>
#include <cstdlib>
#include <ctime>
#include<iostream>
using namespace std;
CSP_Queens::CSP_Queens(int numOfQueens)
{
srand((unsigned)time(NULL));
N = numOfQueens;
row = new int[N];
col = new int[N];
pdiag=new int[2 * N];
cdiag=new int[2 * N];
R=new int[N];
}
CSP_Queens::~CSP_Queens()
{
if (NULL != row)delete[]row;
if (NULL != col)delete[]col;
if (NULL != pdiag)delete[]pdiag;
if (NULL != cdiag)delete[]cdiag;
if (NULL != R)delete[]R;
}
int CSP_Queens::swap(int &a, int &b)
{
int t = a; a = b; b = t;
return 0;
}
//
int CSP_Queens::GetP(int row, int col)
{
return row - col + N - 1;
}
int CSP_Queens::GetC(int row, int col)
{
return row + col;
}
//返回begin, begin + 1, ... , end - 1 这end - begin个数中的随机的一个
int CSP_Queens::My_rand(int begin, int end)//左闭右开[begin, end)
{
return rand() % (end - begin) + begin;
}
//原地shuffle算法,算法导论中的randomize in place算法
void CSP_Queens::Randomize(int a[], int begin, int end)// 左闭右开
{
for (int i = begin; i <= end - 2; i++){
int x = My_rand(i, end);
swap(a[i], a[x]);
}
}
//初始化皇后的摆放,同时初始化row,col,pdiag,cdiag数组
void CSP_Queens::Init()
{
for (int i = 0; i < N; i++){//首先全部安放在主对角线上
R[i] = i;
}
//下面随机抽取调换两行皇后位置
Randomize(R, 0, N);//初始化N个皇后对应的R数组为0~N-1的一个排列,
//此时 即没有任意皇后同列,也没有任何皇后同行
for (int i = 0; i < N; i++){
row[i] = 1;//每行恰好一个皇后
col[i] = 0;
}
for (int i = 0; i < 2 * N - 1; i++){
pdiag[i] = 0;
cdiag[i] = 0;
}
//初始化当前棋局的皇后所在位置的各个冲突数
for (int i = 0; i < N; i++){
col[R[i]]++;
pdiag[GetP(i, R[i])]++;
cdiag[GetC(i, R[i])]++;
}
}
//用最小冲突算法调整第row行的皇后的位置(初始化时每行都有一个皇后,调整后仍然在第row行)
//调整过后check一下看看是否已经没有冲突,如果没有冲突(达到终止状态),返回true
bool CSP_Queens::Adjust_row(int row)
{
int cur_col = R[row];
int optimal_col = cur_col;//最佳列号,设置为当前列,然后更新
int min_conflict = col[optimal_col] + pdiag[GetP(row, optimal_col)] - 1
+ cdiag[GetC(row, optimal_col)] - 1;//对角线冲突数为当前对角线皇后数减一
for (int i = 0; i < N; i++) {//逐个检查第row行的每个位置
if (i == cur_col) {
continue;
}
int conflict = col[i] + pdiag[GetP(row, i)] + cdiag[GetC(row, i)];
if (conflict < min_conflict) {
min_conflict = conflict;
optimal_col = i;
}
}
if (optimal_col != cur_col) {//要更新col,pdiag,cdiag
col[cur_col]--;
pdiag[GetP(row, cur_col)]--;
cdiag[GetC(row, cur_col)]--;
col[optimal_col]++;
pdiag[GetP(row, optimal_col)]++;
cdiag[GetC(row, optimal_col)]++;
R[row] = optimal_col;
if (col[cur_col] == 1 && col[optimal_col] == 1
&& pdiag[GetP(row, optimal_col)] == 1 && cdiag[GetC(row, optimal_col)] == 1) {
return Qualify();//qualify相对更耗时,所以只在满足上面基本条件后才检查
}
}
//当前点就是最佳点,一切都保持不变
return false;//如果都没变的话,肯定不满足终止条件,否则上一次就应该返回true并终止了
}
//检查冲突
bool CSP_Queens::Qualify()
{
for (int i = 0; i < N; i++){
if (col[R[i]] != 1 ||
pdiag[GetP(i, R[i])] != 1 ||
cdiag[GetC(i, R[i])] != 1) {
return false;
}
}
return true;
}
void CSP_Queens::Print_result()
{
cout << "-------结果为:" << endl;
cout << endl;
for (int j = 0; j < N; j++) {
for (int k = 0; k < N; k++) {
if (R[j] == k)
cout << "Q";
else
cout << "+";
cout << " ";
}
cout << endl;
}
}
//最终用户调用函数,numOfQueens为输入皇后数,PrintChessBoard判断是否输出棋盘表示
int CSP_Queens::CSPAlgorithms(bool PrintChessBord)
{
srand((unsigned)time(NULL));
Init();
if (Qualify()) {//运气很好,初始化后就满足终止条件
Print_result();
return 0;
}
bool end = false;
while (!end) {
for (int i = 0; i < N; i++) {
if (Adjust_row(i)) {
end = true;
break;
}
}
}
Print_result();
return 0;
}
Source.cpp
//Source.cpp
#include <ctime>
#include<iostream>
#include"CSPAlgorithms.h"
using namespace std;
int main(int argc, const char *argv[])
{
bool end = false;
while (!end) {
cout << "-----------CSPAlgorithms---------" << endl;
cout << "--------------请输入皇后数:";
int N;
cin >> N;
int time1 = clock();
CSP_Queens myQueens(N);
myQueens.CSPAlgorithms(end);
int time2 = clock();
cout << "---" << N << "皇后问题耗时:" << time2 - time1 << " ms" << endl;
char p;
cout << "是否继续测试?(y/n):";
cin >> p;
if (p == 'n')break;
}
return 0;
}

