人工智能课程设计报告-罗马尼亚问题
人工智能课程设计报告
- 班级:____________________
- 姓名:____________________
- 学号:____________________
- 指导教师:赵曼
- 2015年11月
课程背景
人工智能(Artificial Intelligence),英文缩写为AI。它是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。 人工智能是计算机科学的一个分支,它企图了解智能的实质,并生产出一种新的能以人类智能相似的方式做出反应的智能机器,该领域的研究包括机器人、语言识别、图像识别、自然语言处理和专家系统等。人工智能从诞生以来,理论和技术日益成熟,应用领域也不断扩大,可以设想,未来人工智能带来的科技产品,将会是人类智慧的“容器”。
人工智能是对人的意识、思维的信息过程的模拟。人工智能不是人的智能,但能像人那样思考、也可能超过人的智能。
人工智能是一门极富挑战性的科学,从事这项工作的人必须懂得计算机知识,心理学和哲学。人工智能是包括十分广泛的科学,它由不同的领域组成,如机器学习,计算机视觉等等,总的说来,人工智能研究的一个主要目标是使机器能够胜任一些通常需要人类智能才能完成的复杂工作。但不同的时代、不同的人对这种“复杂工作”的理解是不同的。
人工智能是计算机学科的一个分支,二十世纪七十年代以来被称为世界三大尖端技术之一(空间技术、能源技术、人工智能)。也被认为是二十一世纪三大尖端技术(基因工程、纳米科学、人工智能)之一。这是因为近三十年来它获得了迅速的发展,在很多学科领域都获得了广泛应用,并取得了丰硕的成果,人工智能已逐步成为一个独立的分支,无论在理论和实践上都已自成一个系统。
人工智能是研究使计算机来模拟人的某些思维过程和智能行为(如学习、推理、思考、规划等)的学科,主要包括计算机实现智能的原理、制造类似于人脑智能的计算机,使计算机能实现更高层次的应用。人工智能将涉及到计算机科学、心理学、哲学和语言学等学科。可以说几乎是自然科学和社会科学的所有学科,其范围已远远超出了计算机科学的范畴,人工智能与思维科学的关系是实践和理论的关系,人工智能是处于思维科学的技术应用层次,是它的一个应用分支。从思维观点看,人工智能不仅限于逻辑思维,要考虑形象思维、灵感思维才能促进人工智能的突破性的发展,数学常被认为是多种学科的基础科学,数学也进入语言、思维领域,人工智能学科也必须借用数学工具,数学不仅在标准逻辑、模糊数学等范围发挥作用,数学进入人工智能学科,它们将互相促进而更快地发展。
题目一:罗马利亚度假问题
问题描述
分别用代价一致的宽度优先、有限制的深度优先(预设搜索层次)、贪婪算法和A*算法求解“罗马利亚度假问题”。即找到从初始地点 Arad到 目的地点 Bucharest 的一条路径。
要求: 分别用文件存储地图和启发函数表,用生成节点数比较几种算法在问题求解时的效率,并列表给出结果。
数据如下: 1、地图 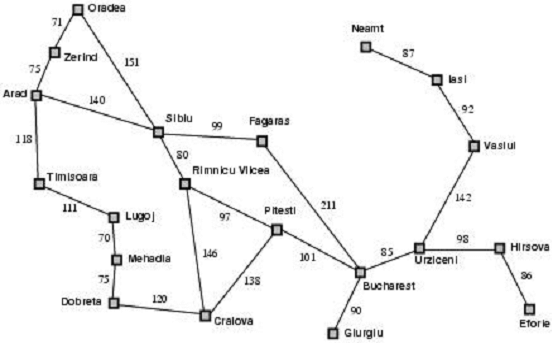 2、启发函数值 Arad 366 Mehadia 241 Bucharest 0 Neamt 234 Craiova 160 Oradea 380 Doberta 242 Pitesti 100 Eforie 161 Rimmicu_Vikea 193 Fagaras 176 Sibiu 253 Glurgiu 77 Timisoara 329 Hirsova 151 Urziceni 80 Iasi 226 Vaslui 199 Lugoj 244 Zerind 374
2、启发函数值 Arad 366 Mehadia 241 Bucharest 0 Neamt 234 Craiova 160 Oradea 380 Doberta 242 Pitesti 100 Eforie 161 Rimmicu_Vikea 193 Fagaras 176 Sibiu 253 Glurgiu 77 Timisoara 329 Hirsova 151 Urziceni 80 Iasi 226 Vaslui 199 Lugoj 244 Zerind 374
3、地图数据表
0 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 140 1000 118 1000 1000 1000 1000 1000 75
1000 0 1000 1000 1000 1000 75 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 70 1000
1000 1000 0 1000 1000 1000 1000 101 1000 1000 211 1000 90 1000 1000 85 1000 1000 1000 1000
1000 1000 1000 0 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 87 1000 1000 1000
1000 1000 1000 1000 0 1000 120 138 1000 146 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000
1000 1000 1000 1000 1000 0 1000 1000 1000 1000 1000 151 1000 1000 1000 1000 1000 1000 1000 71
1000 75 1000 1000 120 1000 0 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000
1000 1000 101 1000 138 1000 1000 0 1000 97 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000
1000 1000 1000 1000 1000 1000 1000 1000 0 1000 1000 1000 1000 1000 86 1000 1000 1000 1000 1000
1000 1000 1000 1000 146 1000 1000 97 1000 0 1000 80 1000 1000 1000 1000 1000 1000 1000 1000
1000 1000 211 1000 1000 1000 1000 1000 1000 1000 0 99 1000 1000 1000 1000 1000 1000 1000 1000
140 1000 1000 1000 1000 151 1000 1000 1000 80 99 0 1000 1000 1000 1000 1000 1000 1000 1000
1000 1000 90 1000 1000 1000 1000 1000 1000 1000 1000 1000 0 1000 1000 1000 1000 1000 1000 1000
118 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 0 1000 1000 1000 1000 111 1000
1000 1000 1000 1000 1000 1000 1000 1000 86 1000 1000 1000 1000 1000 0 98 1000 1000 1000 1000
1000 1000 85 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 98 0 1000 1000 1000 1000
1000 1000 1000 87 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 0 92 1000 1000
1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 92 0 1000 1000
1000 70 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 111 1000 1000 1000 1000 0 1000
75 1000 1000 1000 1000 71 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 0
算法分析
1) 宽度优先搜索算法
广度优先搜索使用队列(queue)来实现
- 把根节点放到队列的末尾。
- 每次从队列的头部取出一个元素,查看这个元素所有的下一级元素,把它们放到队列的末尾。并把这个元素记为它下一级元素的前驱。
- 找到所要找的元素时结束程序。
- 如果遍历整个图还没有找到,结束程序。
2) 深度优先搜索算法
深度优先搜索用栈(stack)来实现,整个过程可以想象成一个倒立的树形:
- 把根节点压入栈中。
- 每次从栈中弹出一个元素,搜索所有在它下一级的元素,把这些元素压入栈中。并把这个元素记为它下一级元素的前驱。
- 找到所要找的元素时结束程序。
- 如果遍历整个树还没有找到,结束程序。
3) 贪婪算法
- 建立数学模型来描述问题
- 把求解的问题分成若干个子问题。
- 对每一子问题求解,得到子问题的局部最优解。
- 把子问题的解局部最优解合成原来解问题的一个解。
实现该算法的过程: 从问题的某一初始解出发; while 能朝给定总目标前进一步 do 求出可行解的一个解元素; 由所有解元素组合成问题的一个可行解。
4) A*算法
A*[1] (A-Star)算法是一种静态路网中求解最短路最有效的直接搜索方法。
公式表示为: f(n)=g(n)+h(n),
- 其中 f(n) 是从初始点经由节点n到目标点的估价函数,
- g(n) 是在状态空间中从初始节点到n节点的实际代价,
- h(n) 是从n到目标节点最佳路径的估计代价。
- 保证找到最短路径(最优解的)条件,关键在于估价函数f(n)的选取:
- 估价值h(n)<= n到目标节点的距离实际值,这种情况下,搜索的点数多,搜索范围大,效率低。但能得到最优解。并且如果h(n)=d(n),即距离估计h(n)等于最短距离,那么搜索将严格沿着最短路径进行, 此时的搜索效率是最高的。 如果 估价值>实际值,搜索的点数少,搜索范围小,效率高,但不能保证得到最优解。
二、 数据结构
1) 图结构:
 实现存储“罗马尼亚度假问题”的图空间;
实现存储“罗马尼亚度假问题”的图空间;
抽象图结构的实现:
typedef struct //图节点类型
{
char cityname[20];
int value;
int cost;
}Ver;
class Graph //图结构
{
public:
Graph();
~Graph();
Ver V[MaxV];
int edge[MaxV][MaxV];
int numofedges; //注意这个变量的引用位置
//读取地图节点信息
void ReadVertex();
//读取地图边关系信息
void ReadEdge();
//取与第V个节点的第一个邻接点
int GetFirstVertex(int v);
//找到第V1个节点的V2之后的下一个邻接节点
int GetNextVertex(int v1, int v2);
int GetVerValue(int index);//获取V[index] 的ver 的value值
int GetVerCost(int index);//获取V[index] 的ver 的cost 值
int GetEdge(int row, int col);//获取edge[row][col] 的值
void SetVerCost(int index,int cost);
};
2)队列结构
 宽度优先算法以及A*算法 使用到。
宽度优先算法以及A*算法 使用到。
抽象队列结构实现:
class SeqQueue
{
public:
SeqQueue();
~SeqQueue();
void QueueInitiate();
int QueueNotEmpty();
int QueueAppend(int x);
int QueueDelete(int *d);
int QueueOrderAppend(int x, Graph &G);
//A*算法使用
int Queue_A_OrderAppend(int x, Graph &G);
private:
int queue[MaxSize];
int rear;
int front;
int count;
};
3)栈结构
 深度优先算法使用; 栈结构的抽象类型实现:
深度优先算法使用; 栈结构的抽象类型实现:
class Stack
{
public:
Stack();
~Stack();
bool StackNotFull();
bool StakNotEmpty();
void StackPop(Graph &G);
void StackPush(int x, Graph &G);
void PrintStack(Graph &G);
int GetWeight();
private:
int a[100];
int top1;
int weight;
};
三.算法设计
1) 宽度优先搜索算法
//宽度优先算法
void Romania_Trip::BroadFirstSearch(Graph &graph, int v)
{
int u, w; i = 0;
SeqCQuene queue;
visited[v] = 1;//访问节点
count++;
if (v == end)return;
queue.QueueAppend( v);//入队列
while (queue.QueueNotEmpty())//队列非空
{
queue.QueueDelete(&u);//取队列节点
w = graph.GetFirstVertex( u);
while (w != -1) //有子节点的话
{
if (!visited[w])//如果子节点未被访问,则访问子节点
{
Visit(w, u);
visited[w] = 1;
count++;
if (w == end)//找到结果
{
Print(graph, b, end, v);
return;
}
queue.QueueAppend(w);//节点压入队列
}
w = graph.GetNextVertex(u, w);
}
}
}
2) 深度优先搜索算法
//深度优先算法
bool isOK = false;
int level = 0;
const int Level = 8;//预设的搜索层次
void Romania_Trip::DepthFirstSearch(Graph &graph, int v, Stack &stack)
{
int w; i = 0;
if (isOK == true)return;
if (level+1 > Level)return;//大于搜索层次时不再深入
level++;
visited[v] = 1;//访问该节点
count++;
stack.StackPush(v, graph);
if (v == end || stack.GetWeight() >= MaxWeight)
{
w = -1;
if (v == end&&stack.GetWeight() <= MaxWeight)
{
cout << "---深度优先遍历路径为:";
stack.PrintStack(graph);
/*if (MaxWeight>stack.GetWeight())
MaxWeight = stack.GetWeight();*/
cout << "---路径长度为:" << stack.GetWeight() << endl
<< "---访问节点数为:" << count << endl
<<"---搜索层次:"<<level<<endl;
isOK = true;
}
}
else
{
w = graph.GetFirstVertex(v);//取当前节点的第一个子节点
}
while (w != -1)
{
if (!visited[w])
DepthFirstSearch(graph, w, stack);//递归访问
w = graph.GetNextVertex(v, w);//取当前节点的下一个子节点
}
visited[v] = 0;//返回时置该节点为未访问
stack.StackPop( graph);//将该节点弹出栈,并根据graph 中weight 的值更改当前栈值
level--;
}
3)贪婪算法
//贪婪算法
void Romania_Trip::Greedy_Algorithms(Graph &graph, int v)
{
int u, w;
SeqCQuene queue;//队列存储图节点在图中的索引值,优先队列,value小的在队头
visited[v] = 1;
if (v == end){ return; }
queue.QueueOrderAppend( v, graph);//图节点按优先顺序入队列
count++; //访问节点数+1
while (queue.QueueNotEmpty())//宽度优先,循环
{
queue.QueueDelete( &u);//删除队列头元素并返回删除的数值
//cout << "u= " << u << " ";
w = graph.GetFirstVertex(u);
while (w != -1)
{
if (!visited[w])
{
Visit(w, u);//访问w节点,将way b 的指向更新
if (w == end)
{
//cout << "w==end";
count++;
return;
}
queue.QueueOrderAppend( w, graph); //图节点按优先顺序入队列
count++;
}
w = graph.GetNextVertex(u, w);
}
}
}
4)A*算法
//A*算法
void Romania_Trip::AStar_Algorithms(Graph &graph, int v)
{
//i = 0; count = 0;
int u, w;
SeqCQuene queue;
if (v == end) return;//到达终点
queue.Queue_A_OrderAppend(v, graph);
count++;
while (queue.QueueNotEmpty())
{
queue.QueueDelete( &u);
if (u == end)
{
cout << "---路径长度为:" << graph.GetVerCost(u) + graph.GetVerValue(u) << endl
<< "---访问节点数为:" << count << endl;
return;
}
w = graph.GetFirstVertex( u);
while (w != -1)
{
int cost=graph.GetVerCost(u) + graph.GetEdge(w,u);
graph.SetVerCost(w, cost);//设置当前节点移动到目标节点的预估费用
queue.Queue_A_OrderAppend( w, graph);//按预估费用优先入队列
count++;
w = graph.GetNextVertex(u, w);
}
}
}
四.运行结果及分析
运行结果
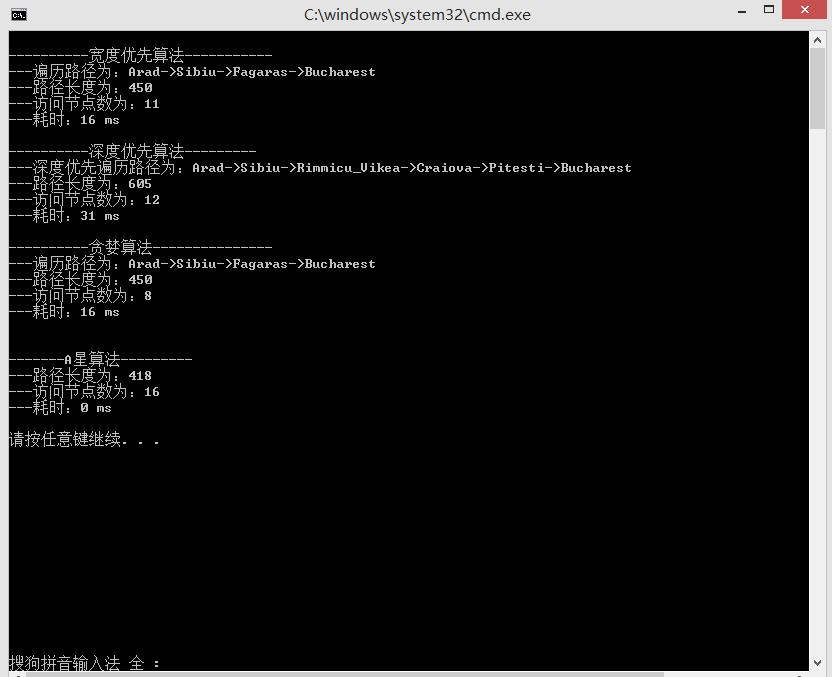
对比:
| 算法 | 节点数 | 路径长度 | 耗时 (ms) | Optimality | Completeness |
|---|---|---|---|---|---|
| BFS | 11 | 450 | 16 | No | Yes |
| DFS | 12 | 605 | 31 | No | No |
| Greedy | 8 | 450 | 16 | No | No |
| A* 算法 | 16 | 418 | 0 | Yes | Yes |
总结:
- Greedy搜索生成的结点数目最少,为8个,效率最高;
- A*算法生成的结点数目最多,为30个,效率最低。
- DFS(一般)、BFS和Greedy搜索找到的都不一定最优解,
- A*算法具有完备性且始终找到的是最优解。
- 宽度优先虽然是完备的(如果分支因子有限的话),在任何情况下宽度优先都能找到一个解,但是,它找到的第一个解并非最优的,
- 此外,最坏的情况是,当目标结点是第d层的最后一个被扩展的结点时,它将耗费大量的时间。
- 宽度优先时间复杂度:
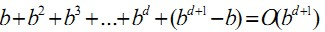 (b为分支因子,d为深度);空间复杂度为所存储的节点的个数。
(b为分支因子,d为深度);空间复杂度为所存储的节点的个数。 - DFS不是完备的(除非查找空间是有限的),同时,它也不能找到最优解。
- 深度优先的时间复杂度:O(b\m);空间复杂度:O(bm+1)(b为分支因子,m为深度,仅有一枝需要存储);
- 贪婪算法不是完备的。同时,它找到的解也不一定是最优解。其时间复杂度:O(b\m)(b代表分支数,m为深度);空间复杂度为O(b\m)。
- 所以只有A*算法和DFS(回溯+剪枝)是完备的,且能够找到最优解;其时间复杂度:扩展节点的数目;空间复杂度:所有生成的结点。
- 综合来看,BFS和贪婪算法的效率较高,但解并非最优,而A*算法的效率稍逊色,但解为最优;
- DFS(回溯+剪枝)搜索虽能找到最优解但效率最低。
